Věta o kinetické a potenciální energii. Open Library - otevřená knihovna vzdělávacích informací

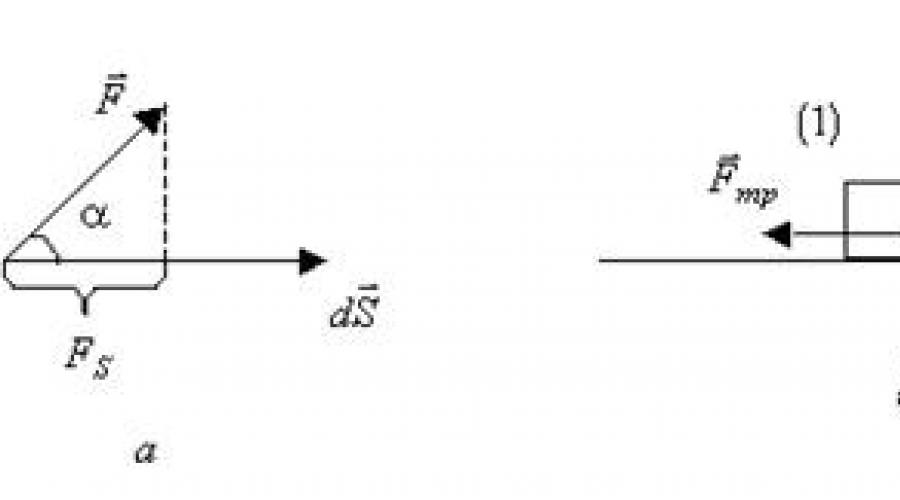
Při elementární práci dA, kterou vykoná síla na elementární posunutí, se nazývá hodnota rovna skalárnímu součinu na

kde úhel a je úhel mezi vektory síly a posunutím (obr. 1.22, a);

Modul vektoru elementárního posunutí nebo elementární dráha prošel bod použití síly.

Práce síly na konečném přemístění se rovná součtu základních prací:

. (1.61)

Pokud je síla konstantní ( =const), pak její práce na přímém úseku délky l bude zapsána takto:

. (1.62)

Práce síly může být kladná, záporná nebo nulová. Práce konstantních sil působících na těleso (obr. 1.22b) na vodorovném řezu dráhy l je tedy rovna:

Představit pojem Kinetická energie W k těles, zapište elementární práci dA síly v jiné formě (viz 1.2.2):

Pak pro práci síly, převádějící těleso ze stavu 1 (rychlost těla) do stavu 2 (rychlost těla), můžeme napsat:

Ze získaného vzorce vyplývá, že práce síly je rovna rozdílu dvou veličin, které určují počáteční (rychlost) a konečný (rychlostní) stav tělesa. V tomto případě přechodové podmínky ze stavu 1 do stavu 2 nemají vliv na písemný projev. Můžeme tedy zavést stavovou funkci tělesa, jeho kinetickou energii W k as SPV, která charakterizuje schopnost těla vykonávat práci v důsledku změny rychlosti jeho pohybu a rovná se

V tomto výrazu je zvolena konstantní hodnota za předpokladu, že při nulové rychlosti tělesa je jeho kinetická energie nulová, proto

Kinetická energie těles nezávisí na tom, jak bylo dosaženo dané rychlosti u, je funkcí stavu tělesa, kladná hodnota, závisí na volbě vztažné soustavy.

Zavedení W to nám umožňuje formulovat větu o kinetické energii, podle níž se algebraický součet práce všech sil působících na těleso rovná přírůstku kinetické energie tělesa:

Tato věta je široce používána k analýze interakce těles nejen v mechanice, ale také v jiných částech kurzu fyziky, jako je elektrostatika, stejnosměrný proud, elektromagnetismus, oscilace a vlny atd.

1.4.2. Kinetická energie rotujícího a.t.t.

Vezměme a.t.t. rotující kolem pevné osy s úhlovou rychlostí (obr. 1.16, b). Představme si těleso jako soubor m.t. masy dm, pak pro kinetickou energii tělesa můžeme napsat:

Takže kinetická energie a.t.t. otáčení kolem pevné osy otáčení, je určeno vzorcem

Účastní-li se těleso současně translačních (rovinných) a rotačních pohybů (například pohyb válce bez klouzání po rovině, obr. 1.23, a), lze získat jeho kinetickou energii

Obr.1.23

jako součet kinetické energie translačního pohybu tělesa spolu s osou rotace procházející jeho těžištěm (bodem Ó), s rychlostí a rotační pohyb tělesa kolem této osy s úhlovou rychlostí

. (1.67)

Za pevnou ( já 1=1/2mR 2) a tenkostěnné ( já 2=mR 2) válce o stejné hmotnosti m a poloměr R kinetické energie se zapisují takto:

.

Získané vzorce pro kinetickou energii válců umožňují vysvětlit experiment na rozdílu doby jejich kutálení po nakloněné rovině o výšce h a délka l(obr. 1.23, b). Takže podle zákona zachování energie (třecí sílu při pohybu válců lze prakticky zanedbat) získáme

,

kde označují rychlosti plného a dutého válce na základně nakloněné roviny.

Když se válce valí, střed jejich hmoty se pohybuje rovnoměrně bez počáteční rychlosti, a proto podle vzorce (1.13) můžeme napsat:

,

těch. Dutý válec se odvaluje déle než válec plný.

Kvalitativně to lze vysvětlit tím, že dutý válec je inertnější než pevný (u něj je moment setrvačnosti kolem osy rotace větší), a proto mění svou rychlost pomaleji, a proto tráví více času valící se po nakloněné rovině.

Jak je vidět z obr. 1.23, a, moduly rychlostí bodů na povrchu válce budou různé. (u B \u003d 0, , u A \u003d 2u) vzhledem k tomu, že se tyto body účastní současně translačních i rotačních pohybů s rychlostmi a , a pro každý bod směřuje tečně k povrchu válce a je roven absolutní hodnotě u( ).

Všimněte si, že pohyb válce lze také považovat za sérii po sobě jdoucích rotací kolem okamžité osy procházející bodem Z(obr. 1.23, a) s úhlovou rychlostí w. Navíc v tomto případě je kinetická energie tělesa také určena vzorcem (1.67).

energie nazývaná skalární fyzikální veličina, což je jediná míra různé formy pohyb hmoty a míra přechodu pohybu hmoty z jedné formy do druhé.

Pro charakterizaci různých forem pohybu hmoty jsou představeny odpovídající druhy energie, např.: mechanická, vnitřní, energie elektrostatické, intranukleární interakce atd.

Energie se řídí zákonem zachování, což je jeden z nejdůležitějších přírodních zákonů.

Mechanická energie E charakterizuje pohyb a interakci těles a je funkcí rychlostí a vzájemných poloh těles. Je rovna součtu kinetických a potenciálních energií.

Kinetická energie

Uvažujme případ, kdy je hmotné těleso m působí konstantní síla \(~\vec F\) (může být výslednicí více sil) a vektory síly \(~\vec F\) a posunutí \(~\vec s\) směřují po jedné přímce čára v jednom směru. V tomto případě lze práci vykonanou silou definovat jako A = F∙s. Modul síly podle druhého Newtonova zákona je F = m∙a a posuvný modul s s rovnoměrně zrychleným přímočarým pohybem je spojen s moduly iniciály υ 1 a konečná υ 2 rychlosti a zrychlení A\(~s = \frac(\upsilon^2_2 - \upsilon^2_1)(2a)\) .

Takže do práce se dostaneme

\(~A = F \cdot s = m \cdot a \cdot \frac(\upsilon^2_2 - \upsilon^2_1)(2a) = \frac(m \cdot \upsilon^2_2)(2) - \frac (m \cdot \upsilon^2_1)(2)\) . (jeden)

Nazýváme fyzikální veličinu rovnající se polovině součinu hmotnosti tělesa a druhé mocniny jeho rychlosti kinetickou energii těla.

Kinetická energie je označena písmenem E k .

\(~E_k = \frac(m \cdot \upsilon^2)(2)\) . (2)

Pak lze rovnost (1) zapsat v následujícím tvaru:

\(~A = E_(k2) - E_(k1)\) . (3)

Věta o kinetické energii

práce výsledných sil působících na těleso se rovná změně kinetické energie tělesa.

Protože změna kinetické energie je rovna práci síly (3), vyjadřuje se kinetická energie tělesa ve stejných jednotkách jako práce, tedy v joulech.

Je-li počáteční rychlost tělesné hmoty m je nula a těleso zvýší svou rychlost na hodnotu υ , pak se práce síly rovná konečné hodnotě kinetické energie tělesa:

\(~A = E_(k2) - E_(k1)= \frac(m \cdot \upsilon^2)(2) - 0 = \frac(m \cdot \upsilon^2)(2)\) . (čtyři)

Fyzikální význam kinetické energie

Kinetická energie tělesa pohybujícího se rychlostí υ ukazuje, jakou práci musí vykonat síla působící na těleso v klidu, aby mu dala tuto rychlost.

Potenciální energie

Potenciální energie je energie vzájemného působení těles.

Potenciální energie tělesa zvednutého nad Zemí je energií interakce mezi tělesem a Zemí působením gravitačních sil. Potenciální energie elasticky deformovaného tělesa je energie vzájemného působení jednotlivých částí tělesa pružnými silami.

Potenciál volala síla, jehož práce závisí pouze na počáteční a konečné poloze pohybujícího se hmotného bodu nebo tělesa a nezávisí na tvaru trajektorie.

Při uzavřené dráze je práce potenciální síly vždy nulová. Mezi potenciální síly patří gravitační síly, elastické síly, elektrostatické síly a některé další.

Síly, jejichž práce závisí na tvaru trajektorie, se nazývají nepotencionální. Při pohybu hmotného bodu nebo tělesa po uzavřené trajektorii není práce nepotencionální síly rovna nule.

Potenciální energie interakce tělesa se Zemí

Najděte práci vykonanou gravitací F t při pohybu tělesa s hmotou m svisle dolů z výšky h 1 nad povrchem Země do výšky h 2 (obr. 1). Pokud rozdíl h 1 – h 2 je zanedbatelná ve srovnání se vzdáleností do středu Země, pak gravitační silou F m při pohybu tělesa lze považovat za konstantní a rovné mg.

Protože posunutí se shoduje ve směru s vektorem gravitace, práce vykonaná gravitací je

\(~A = F \cdot s = m \cdot g \cdot (h_1 - h_2)\) . (5)

Uvažujme nyní pohyb tělesa po nakloněné rovině. Při pohybu tělesa po nakloněné rovině (obr. 2) gravitace F t = m∙g dělá práci

\(~A = m \cdot g \cdot s \cdot \cos \alpha = m \cdot g \cdot h\) , (6)

kde h je výška nakloněné roviny, s- modul posunutí rovný délce nakloněné roviny.

Pohyb těla z bodu V přesně tak Z po jakékoli trajektorii (obr. 3) lze mentálně znázornit jako pohyb po úsecích nakloněných rovin s různou výškou h’, h'' atd. Práce ALE gravitace úplně ven V v Z se rovná součtu práce na jednotlivých úsecích cesty:

\(~A = m \cdot g \cdot h" + m \cdot g \cdot h"" + \ldots + m \cdot g \cdot h^n = m \cdot g \cdot (h" + h"" + \ldots + h^n) = m \cdot g \cdot (h_1 - h_2)\) , (7)

kde h 1 a h 2 - výšky od povrchu Země, na kterých se body nacházejí, resp V a Z.

Rovnost (7) ukazuje, že gravitační práce nezávisí na dráze tělesa a je vždy rovna součinu modulu tíže a rozdílu výšek v počáteční a konečné poloze.

Při pohybu dolů je práce gravitace kladná, při pohybu nahoru záporná. Práce gravitace na uzavřené dráze je nulová.

Rovnost (7) může být reprezentována takto:

\(~A = - (m \cdot g \cdot h_2 - m \cdot g \cdot h_1)\) . (osm)

Fyzikální veličina rovnající se součinu hmotnosti tělesa modulem zrychlení volného pádu a výškou, do které je těleso zvednuto nad povrch Země, se nazývá potenciální energie interakce mezi tělem a zemí.

Práce gravitace při pohybu tělesa s hmotou m z bodu ve výšce h 2, do bodu umístěného ve výšce h 1 od povrchu Země, podél jakékoli trajektorie se rovná změně potenciální energie interakce mezi tělesem a Zemí, brané s opačným znaménkem.

\(~A = - (E_(p2) - E_(p1))\) . (9)

Potenciální energie je označena písmenem E p .

Hodnota potenciální energie tělesa vyvýšeného nad Zemí závisí na volbě nulové úrovně, tedy výšky, ve které se předpokládá, že potenciální energie je nulová. Obvykle se předpokládá, že potenciální energie tělesa na povrchu Země je nulová.

S touto volbou nulové úrovně, potenciální energie E p tělesa ve výšce h nad povrchem Země, se rovná součinu hmotnosti m tělesa a modulu zrychlení volného pádu G a vzdálenost h to z povrchu Země:

\(~E_p = m \cdot g \cdot h\) . (deset)

Fyzikální význam potenciální energie interakce těla se Zemí

Potenciální energie tělesa, na které působí gravitace, se rovná práci, kterou gravitace vykoná při pohybu tělesa na nulovou úroveň.

Na rozdíl od kinetické energie translačního pohybu, která může mít pouze kladné hodnoty, může být potenciální energie tělesa buď kladná, nebo záporná. tělesná hmota m ve výšce h, kde h < h 0 (h 0 - nulová výška), má negativní potenciální energii:

\(~E_p = -m \cdot g \cdot h\) .

Potenciální energie gravitační interakce

Potenciální energie gravitační interakce soustavy dvou hmotných bodů s hmotami m a M umístěné na dálku r jeden od druhého se rovná

\(~E_p = G \cdot \frac(M \cdot m)(r)\) . (jedenáct)

kde G je gravitační konstanta a nula referenční potenciální energie ( E p = 0) je přijato pro r = ∞.

Potenciální energie gravitační interakce tělesa s hmotou m se zemí kde h je výška tělesa nad zemským povrchem, M e je hmotnost Země, R e je poloměr Země a nula potenciální energie je zvolena na h = 0.

\(~E_e = G \cdot \frac(M_e \cdot m \cdot h)(R_e \cdot (R_e +h))\) . (12)

Za stejné podmínky výběru referenční nuly, potenciální energie gravitační interakce tělesa s hmotou m se Zemí pro nízké nadmořské výšky h (h « R e) se rovná

\(~E_p = m \cdot g \cdot h\) ,

kde \(~g = G \cdot \frac(M_e)(R^2_e)\) je modul gravitačního zrychlení blízko zemského povrchu.

Potenciální energie elasticky deformovaného tělesa

Vypočítejme práci, kterou vykoná pružná síla, když se deformace (prodloužení) pružiny změní z nějaké počáteční hodnoty X 1 na konečnou hodnotu X 2 (obr. 4, b, c).

Pružná síla se mění s deformací pružiny. Chcete-li najít práci pružné síly, můžete vzít průměrnou hodnotu modulu síly (protože elastická síla závisí lineárně na X) a vynásobte modulem posunutí:

\(~A = F_(upr-cp) \cdot (x_1 - x_2)\) , (13)

kde \(~F_(upr-cp) = k \cdot \frac(x_1 - x_2)(2)\) . Odtud

\(~A = k \cdot \frac(x_1 - x_2)(2) \cdot (x_1 - x_2) = k \cdot \frac(x^2_1 - x^2_2)(2)\) nebo \(~A = -\left(\frac(k \cdot x^2_2)(2) - \frac(k \cdot x^2_1)(2) \right)\) . (čtrnáct)

Nazýváme fyzikální veličinu rovnající se polovině součinu tuhosti tělesa a druhé mocniny jeho deformace potenciální energie elasticky deformované tělo:

\(~E_p = \frac(k \cdot x^2)(2)\) . (patnáct)

Ze vzorců (14) a (15) vyplývá, že práce pružné síly se rovná změně potenciální energie elasticky deformovaného tělesa, brané s opačným znaménkem:

\(~A = -(E_(p2) - E_(p1))\) . (16)

Pokud X 2 = 0 a X 1 = X, pak, jak je vidět ze vzorců (14) a (15),

\(~E_p = A\) .

Fyzikální význam potenciální energie deformovaného tělesa

potenciální energie elasticky deformovaného tělesa se rovná práci vykonané elastickou silou, když těleso přejde do stavu, kdy je deformace nulová.

Potenciální energie charakterizuje interagující tělesa a kinetická energie charakterizuje pohybující se tělesa. Potenciální i kinetická energie se mění pouze v důsledku takové interakce těles, při které síly působící na tělesa konají práci jinou než nulovou. Zamysleme se nad otázkou energetických změn při interakcích těles tvořících uzavřený systém.

uzavřený systém je systém, na který nepůsobí vnější síly nebo je působení těchto sil kompenzováno. Jestliže několik těles na sebe vzájemně působí pouze gravitačními a pružnými silami a nepůsobí na ně žádné vnější síly, pak pro jakékoli interakce těles je práce pružných nebo gravitačních sil rovna změně potenciální energie těles, odečtené s opačným znaménkem:

\(~A = -(E_(p2) - E_(p1))\) . (17)

Podle věty o kinetické energii se práce stejných sil rovná změně kinetické energie:

\(~A = E_(k2) - E_(k1)\) . (osmnáct)

Porovnání rovností (17) a (18) ukazuje, že změna kinetické energie těles v uzavřené soustavě se v absolutní hodnotě rovná změně potenciální energie soustavy těles a má opačné znaménko:

\(~E_(k2) - E_(k1) = -(E_(p2) - E_(p1))\) nebo \(~E_(k1) + E_(p1) = E_(k2) + E_(p2) \) . (19)

Zákon zachování energie v mechanických procesech:

součet kinetické a potenciální energie těles, která tvoří uzavřený systém a vzájemně na sebe působí gravitačními a elastickými silami, zůstává konstantní.

Součet kinetických a potenciálních energií těles se nazývá plnou mechanickou energii.

Udělejme jednoduchý experiment. Vyhoďte ocelovou kouli. Když nahlásíme počáteční rychlost υ, dáme jí kinetickou energii, díky které začne stoupat nahoru. Působení gravitace vede ke snížení rychlosti míče, a tím i jeho kinetické energie. Míč ale stoupá výš a výš a získává stále více potenciální energie ( E p= m∙g∙h). Kinetická energie tedy nezmizí beze stopy, ale přemění se na potenciální energii.

V okamžiku dosažení nejvyššího bodu trajektorie ( υ = 0) míč je zcela zbaven kinetické energie ( E k = 0), ale zároveň se jeho potenciální energie stává maximální. Poté míč změní směr a se zvyšující se rychlostí se pohybuje dolů. Nyní dochází ke zpětné přeměně potenciální energie na energii kinetickou.

Odhaluje zákon zachování energie fyzický význam koncepty práce:

práce gravitačních a elastických sil se na jedné straně rovná nárůstu kinetické energie a na druhé straně poklesu potenciální energie těles. Práce se tedy rovná energii přeměněné z jedné formy na druhou.

Zákon o změně mechanické energie

Pokud systém interagujících těles není uzavřený, pak se jeho mechanická energie nešetří. Změna mechanické energie takového systému se rovná práci vnějších sil:

\(~A_(vn) = \Delta E = E - E_0\) . (dvacet)

kde E a E 0 jsou celkové mechanické energie systému v konečném a počátečním stavu.

Příkladem takového systému je systém, ve kterém spolu s potenciálními silami působí i síly nepotencionální. Třecí síly jsou nepotencionální síly. Ve většině případů, kdy úhel mezi třecí silou F r tělo je π radiánů, práce třecí síly je záporná a rovná se

\(~A_(tr) = -F_(tr) \cdot s_(12)\) ,

kde s 12 - dráha těla mezi body 1 a 2.

Třecí síly při pohybu soustavy snižují její kinetickou energii. V důsledku toho mechanická energie uzavřeného nekonzervativního systému vždy klesá a mění se v energii nemechanických forem pohybu.

Například auto pohybující se po vodorovném úseku silnice po vypnutí motoru ujede určitou vzdálenost a zastaví se působením třecích sil. Kinetická energie dopředného pohybu vozu se rovnala nule a potenciální energie se nezvýšila. Při brzdění vozu se zahřívaly brzdové destičky, pneumatiky auta a asfalt. V důsledku působení třecích sil tedy kinetická energie vozu nezmizela, ale přeměnila se ve vnitřní energii tepelného pohybu molekul.

Zákon zachování a přeměny energie

v jakékoli fyzické interakci se energie přeměňuje z jedné formy na druhou.

Někdy úhel mezi silou tření F tr a elementární posunutí Δ r je nula a práce třecí síly je kladná:

\(~A_(tr) = F_(tr) \cdot s_(12)\) ,

Příklad 1. Může vnější síla F působí na baru V, který se dá na vozíku klouzat D(obr. 5). Pokud se vozík pohybuje doprava, pak práce posuvné třecí síly F tr2 působící na vozík ze strany lišty je pozitivní:

Příklad 2. Když se kolo odvaluje, jeho valivá třecí síla směřuje podél pohybu, protože bod kontaktu kola s vodorovným povrchem se pohybuje ve směru opačném ke směru pohybu kola a práce třecí síly je kladná. (obr. 6):

Literatura

1. Kabardin O.F. Fyzika: Ref. materiály: Proc. příspěvek na studenty. - M.: Osvícení, 1991. - 367 s.
2. Kikoin I.K., Kikoin A.K. Fyzika: Proc. pro 9 buněk. prům. škola - M .: Pro-sveshchenie, 1992. - 191 s.
3. Základní učebnice fyziky: Proc. příspěvek. Ve 3 svazcích / Ed. G.S. Landsberg: v. 1. Mechanika. Teplo. Molekulární fyzika. – M.: Fizmatlit, 2004. – 608 s.
4. Yavorsky B.M., Seleznev Yu.A. Referenční příručka fyziky pro uchazeče o studium na vysokých školách a sebevzdělávání. – M.: Nauka, 1983. – 383 s.

Pomocí posuvníků nastavte hodnoty tělesné hmotnostim, úhel sklonu rovinyA, Vnější síla F ext , koeficient třeníma zrychlení A uvedené v tabulce 1 pro váš tým.

Současně spusťte stopky a stiskněte tlačítko "Start". Stopky vypněte ve chvíli, kdy se těleso zastaví na konci nakloněné roviny.

Proveďte tento experiment 10krát a zaznamenejte si výsledky měření doby, kdy tělo sklouzne z nakloněné roviny do tabulky. 2.

TABULKA 1. Počáteční parametry experimentu

TABULKA 2. Výsledky měření a výpočtů

E) - práce třecí síly v úseku klesání;

E) - působení vnější síly na sestupovém úseku

a zapište tyto hodnoty do odpovídajících řádků tabulky. 2. Vypočítejte průměrné hodnoty těchto parametrů a zapište je do sloupce "průměrné hodnoty" v tabulce 2.

Pomocí vzorce (7) ověřte splnění zákona zachování mechanické energie při pohybu tělesa po nakloněné rovině. Vypočítejte chyby a vyvodte závěry na základě výsledků experimentů.

Otázky a úkoly pro sebeovládání

1. Jaký je zákon zachování mechanické energie?

2. Pro které systémy je splněn zákon zachování mechanické energie?

3. Jaký je rozdíl mezi pojmy energie a práce?

4. Co způsobuje změnu potenciální energie?

5. Co způsobuje změnu kinetické energie?

6. Je nutné splnit podmínku uzavřenosti mechanické soustavy těles, aby byl splněn zákon zachování mechanické energie?

7. Jaké síly se nazývají konzervativní?

8. Jaké síly se nazývají disipativní?

9. Tělo je pomalu taženo do kopce. Závisí tvar horského profilu na: a) působení gravitace; b) práce třecí síly? Počáteční a koncové body pohybu těla jsou pevně dané.

10. Těleso sklouzne z vrcholu nakloněné roviny bez počáteční rychlosti. Zastaví se práce třecí síly na celé dráze pohybu tělesa na vodorovném řezu: a) na úhlu sklonu roviny; b) na koeficientu tření?

11. Dvě tělesa kloužou po nakloněné rovině ze stejné výšky: jedno s hmotou m , jiná hmota 2 m . Které z těles urazí větší vzdálenost po vodorovném řezu k zastavení a kolikrát? Koeficienty tření pro obě tělesa jsou stejné.

12.Sáně s hmotností m valil se z hory výšky H a zastavil se na vodorovném úseku. Jakou práci je třeba vykonat, abychom je zvedli na horu podél válcovací čáry.

13. Při stejné počáteční rychlosti projde těleso: a) prohlubeň; b) saně se stejnými oblouky trajektorií a stejnými koeficienty tření. Porovnejte rychlosti tělesa na konci dráhy v obou případech.

Literatura

1. Trofimová T.I. Kurz fyziky. Kap.3, §§12,13.

Začněme definicí. Práce ALE síla F při pohybu X těleso, na které je aplikováno, je definováno jako skalární součin vektorů F a X .

A= F x= Fxcosα. (2.9.1)

Kde α je úhel mezi směry síly a posunutí.

Nyní budeme potřebovat výraz (1.6 a), který jsme získali při rovnoměrně zrychleném pohybu. Ale uděláme univerzální závěr, který se nazývá věta o kinetické energii. Přepišme tedy rovnost (1,6 a)

A· X=(PROTI 2 –PROTI 0 2)/2.

Vynásobením obou stran rovnice hmotností částice dostaneme

fx\u003d m (V 2 -V 0 2) / 2.

Konečně

A= m V 2 /2 - m V 0 2 /2. (2.9.1)

hodnota E= m V 2 /2 se nazývá kinetická energie částice.

Jste zvyklí, že v geometrii mají věty svou vlastní slovní formulaci. Abychom dodrželi tuto tradici, předkládáme větu o kinetické energii ve formě textu.

Změna kinetické energie tělesa se rovná práci všech sil, které na něj působí.

Tato věta je univerzální, to znamená, že platí pro jakýkoli typ pohybu. Jeho přesný důkaz je však spojen s využitím integrálního počtu. Proto jej vynecháváme.

Uvažujme příklad pohybu tělesa v gravitačním poli. Práce gravitace nezávisí na typu trajektorie spojující počáteční a koncový bod, ale je určena pouze rozdílem výšek v počáteční a koncové poloze:

A=mg( h 1 –h 2). (2.9.2)

Vezměme nějaký bod gravitačního pole jako počátek a uvažujme práci vykonanou gravitací při přesunu částice do tohoto bodu z jiného libovolného bodu R ve výšce h. Tato práce je mgh a nazývá se potenciální energie E n částic v bodě R:

E n = mgh (2.9.3)

Nyní transformujeme rovnost (2.9.1), mechanická věta o kinetické energii nabývá tvaru

A= m V 2 /2 - m V 0 2 /2= E p1 - E p2. (2.9.4)

m V 2 /2+ E n2 = m V 0 2 /2+ E n1.

V této rovnosti je na levé straně součet kinetické a potenciální energie v koncovém bodě trajektorie a napravo - v počátečním.

Toto množství se nazývá celková mechanická energie. Označíme to E.

E=E na + E P.

Dospěli jsme k zákonu zachování celkové energie: v uzavřeném systému se celková energie zachovává.

Je však třeba učinit jednu poznámku. Zatímco jsme uvažovali o příkladu tzv konzervativní síly. Tyto síly závisí pouze na poloze v prostoru. A práce vykonaná takovými silami při pohybu tělesa z jedné polohy do druhé závisí pouze na těchto dvou polohách a nezávisí na dráze. Práce vykonávaná konzervativní silou je mechanicky vratná, to znamená, že při návratu těla do původní polohy mění své znaménko. Gravitace je konzervativní síla. V budoucnu se seznámíme s dalšími typy konzervativních sil, například se silou elektrostatické interakce.

Ale v přírodě existují nekonzervativní síly. Například síla kluzného tření. Čím větší je dráha částice, tím větší práci vykoná síla kluzného tření působící na tuto částici. Kromě toho je práce kluzné třecí síly vždy záporná, to znamená, že taková síla nemůže „vrátit“ energii.

U uzavřených systémů se celková energie samozřejmě šetří. Ale pro většinu problémů v mechanice je důležitější speciální případ zákona zachování energie, totiž zákon zachování celkové mechanické energie. Zde je jeho znění.

Pokud na těleso působí pouze konzervativní síly, zachovává se jeho celková mechanická energie definovaná jako součet kinetických a potenciálních energií..

V následujícím budeme potřebovat dvě další důležité rovnosti. Jako vždy nahradíme odvození jednoduchou demonstrací konkrétního případu tíhového pole. Ale podoba těchto rovností bude platná pro všechny konzervativní síly.

Redukujme rovnost (2.9.4) na tvar

A=F∆X= E p1 - E n2 = -( E p.con - E p.začátek)= – ∆U.

Zde jsme práci zhodnotili ALE při pohybu tělesa o vzdálenost ∆ X. Hodnota ∆U, která se rovná rozdílu mezi konečnou a počáteční potenciální energií, se nazývá změna potenciální energie. A výsledná rovnost si zaslouží samostatný řádek a zvláštní číslo. Pospěšme si, abychom mu to přidělili:

A=– ∆U (2.9.5)

Z toho vyplývá matematický vztah mezi silou a potenciální energií:

F= – ∆U/∆ X (2.9.6)

V obecném případě, který nesouvisí s gravitačním polem, je rovnost (2.9.6) nejjednodušší diferenciální rovnicí

F= – dU/ dx.

Uvažujme poslední příklad bez důkazu. Gravitační síla je popsána zákonem univerzální gravitace F(r)= GmM/ r 2 a je konzervativní. Výraz pro potenciální energii gravitačního pole má tvar:

U(r)= – GmM/ r.

Autor: – Podívejme se na jednoduchý případ. Na těleso o hmotnosti m, umístěné na vodorovné rovině, působí po určitou dobu T horizontální síla F. Nedochází k žádnému tření. Co je to dílo síly F?

Student: – Během T těleso se posune o vzdálenost S= AT 2/2, kde A=F/m Vytoužená práce je tedy ALE=F S= F 2 T 2/(2m).

Autor: Vše je správně, pokud předpokládáme, že těleso bylo v klidu, než na něj začala působit síla. Pojďme si úkol trochu zkomplikovat. Nechte těleso, aby se před počátkem síly pohybovalo přímočaře a rovnoměrně určitou rychlostí V 0 , ve shodě s vnější silou. Co je teď práce pro čas? T?

Student: – Pro výpočet posunutí vezmu obecnější vzorec S \u003d V 0 T+AT 2/2, za práci dostanu ALE=F(V 0 T+AT 2/2). Ve srovnání s předchozím výsledkem vidím, že stejná síla produkuje různou práci ve stejných časových intervalech.

Těleso o hmotnosti m klouže po nakloněné rovině s úhlem sklonu α. Součinitel kluzného tření tělesa na rovině k. Na těleso neustále působí horizontální síla F. Jaká je práce této síly, když se těleso posune o vzdálenost S?

Student: – Udělejme zarovnání sil a najdime jejich výslednici. Na těleso působí vnější síla F, dále gravitace, podpůrné reakce a tření.

Student: – Ukazuje se, že práce A = F S cos a je to. Zvyk hledat pokaždé všechny síly mě opravdu zklamal, zvlášť když je v problému uvedena hmotnost a koeficient tření.

Student: – Dílo síly F Už jsem vypočítal: A 1 = F S cos A. Práce gravitace je A 2 \u003d mgS hřích A. Práce třecí síly ... je negativní, protože vektory síly a posunutí jsou opačně směrovány: A 3 \u003d - kmgS cos A. Práce reakční síly N je nula, protože síla a posunutí jsou kolmé. Pravda, moc nerozumím smyslu negativní práce?

Autor: – To znamená, že práce této síly snižuje kinetickou energii tělesa. Mimochodem. Proberme pohyb tělesa znázorněného na obrázku 2.9.1 z pohledu zákona zachování energie. Nejprve najděte celkovou práci všech sil.

Student: - ALE= ALE 1 + ALE 2 + ALE 3=FS cos a+ mgS hříchα–kmgS cosα.

Podle věty o kinetické energii je rozdíl mezi kinetickými energiemi v konečném a počátečním stavu roven práci vykonané na tělese:

E do - E n = ALE.

Student: – Možná to byly jiné rovnice, které s tímto problémem nesouvisely?

Autor: – Ale všechny rovnice by měly dávat stejný výsledek. Faktem je, že potenciální energie je obsažena v latentní formě ve výrazu pro plnou práci. Opravdu si pamatujte A 2 \u003d mgS hříchα=mgh, kde h je výška sestupu těla. Získejte, nyní z věty o kinetické energii, vyjádření zákona zachování energie.

Student: – Protože mgh \u003d U n - U k, kde U n a U k jsou počáteční a konečné potenciální energie těla, máme:

m PROTI n 2 /2 + U n + ALE 1 + ALE 3 = m PROTI až 2/2+ U na.

Student: – To je podle mého názoru snadné. Práce modulu třecí síly je právě rovna množství tepla Q. Proto Q= kmgS cosα.

Student:m PROTI n 2 /2 + U n + ALE 1 – Q= m PROTI až 2/2+ U na.

Autor: – Pojďme nyní zobecnit definici práce. Faktem je, že vztah (2.9.1) platí pouze pro případ konstantní síly. I když existuje mnoho případů, kdy samotná síla závisí na pohybu částice. Uveďte příklad.

Student: – První, co vás napadne, je natažení pružiny. Jak se volný konec pružiny pohybuje, síla se zvyšuje. Druhý příklad souvisí s kyvadlem, které, jak víme, je obtížnější udržet při velkých odchylkách od rovnovážné polohy.

Autor: – Dobrý. Podívejme se na jarní příklad. Pružná síla ideální pružiny je popsána Hookovým zákonem, podle kterého, když je pružina stlačena (nebo natažena) o určitou míru X existuje síla opačná k posunutí, lineárně závislá na X. Napišme Hookův zákon ve formě rovnosti:

F= – k X (2.9.2)

Zde k je pružinová konstanta, X- velikost deformace pružiny. Závislost na pozemku F(X).

Student: Moje kresba je zobrazena na obrázku.

Obr.2.9.2

Levá polovina grafu odpovídá stlačení pružiny a pravá polovina tahu.

Autor: – Nyní vypočítáme práci síly F při pohybu z X= 0 až X= S. Existuje na to obecné pravidlo. Známe-li obecnou závislost síly na posunutí, pak práce na místě od x 1 až x 2 je oblast pod křivkouF(X) v tomto segmentu.

Student: – To znamená, že práce pružné síly při pohybu tělesa z X= 0 až X=S je záporné a jeho modul se rovná ploše pravoúhlého trojúhelníku: ALE= kS2/2.

ALE= k X 2 /2. (2.9.3)

Tato práce se přemění na potenciální energii deformované pružiny.

Příběh.

Rutherford předvedl publiku rozpad radia. Obrazovka zablikala a pak ztmavla.

- Teď vidíš – Rutherford řekl: – že nic není vidět. A proč není nic vidět, uvidíte nyní.

Otázky a úkoly

1. Vyjmenujte situace, se kterými se setkáváte v každodenním životě a ve kterých jsou zapojeny nekonzervativní síly.

2. Pomalu zvednete knihu ze stolu na vysokou polici. Vyjmenujte síly působící na knihu a určete, které z nich jsou konzervativní a které ne.

3. Výsledná síla působící na částici je konzervativní a zvyšuje její kinetickou energii o 300 J. Jaká je změna a) potenciální energie částice, b) její celkové energie?

4. Má následující tvrzení fyzikální smysl: použití tyčí vyrobených z pružného plastu ve skocích do výšky vedlo ke zvýšení výsledků díky tomu, že jejich větší flexibilita dává dodatečnou elastickou energii, která se přeměňuje na potenciální energii gravitačního pole? ?

5. Existuje nakloněná rovina, jejíž jeden konec je zvednutý do výšky H. tělesná hmota M roluje dolů (bez počáteční rychlosti) z horního bodu. Závisí rychlost tohoto tělesa u paty nakloněné roviny na úhlu, který svírá s horizontem, jestliže a) nedochází ke tření, b) dochází ke tření?

6. Proč jsme stále unavení, když nejprve vylezeme na horu a pak z ní sestoupíme? Vždyť celková práce v gravitačním poli je nulová.

7. Tento příklad je ještě těžší. Představte si, že držíte činku na délku paže. Nebojte se, není moc těžký. Ale přesto se ruka unaví. A není tam žádná mechanická práce, protože tam není žádný pohyb. Kde se utrácí energie vašich svalů?

8. Jarní mše m stojí vzpřímeně na stole. Bude se moci pružina odrazit od stolu poté, co ji stlačíte shora a poté ji uvolníte? Vysvětlete svou odpověď pomocí zákona zachování energie.

9. Co se stane s potenciální energií, kterou měla voda na vrcholu vodopádu, když voda dosáhne dna? A co se stane s kinetickou a celkovou energií?

10. Zkušení turisté raději překročí spadlý kmen, než aby na něj šlápli a seskočili z opačné strany. Vysvětlete jev.

11. Dva lidé jsou na různých plošinách, které se vůči sobě pohybují rychlostí V. Sledují kládu taženou po hrubém vodorovném povrchu. Shodují se hodnoty získané těmito lidmi: a) s kinetickou energií klády; b) celkovou práci vykonanou na těle; c) mechanická energie přeměněná na teplo v důsledku přítomnosti tření? Je odpověď na otázku c) v rozporu s odpověďmi na otázky a) ab)?

12. Odkud se bere kinetická energie auta při jeho rovnoměrném zrychlení z klidu? Jak vztáhnout nárůst kinetické energie do souvislosti s přítomností třecí síly mezi pneumatikami a dálnicí?

13. V zimě se Země přibližuje ke Slunci na nejkratší vzdálenost. Kdy je potenciální energie Země největší?

14 Může být celková mechanická energie záporná? Dát příklad.

15. V jakém bodě je velikost síly největší? U každého očíslovaného bodu uveďte, kterým směrem síla působí. Který bod odpovídá rovnovážné poloze?

Úkoly

16. Kulka prorazí pevnou desku minimální rychlostí 200 slečna. Jakou rychlostí musí letět kulka, aby prorazila toto prkno zavěšené na dlouhé niti? Hmotnost střely 15 G, hmotnost desky 90 G kulka zasáhne přesně střed desky kolmo k jejímu povrchu.

17. Dřevěná kuličková hmota M =1 kg visí na šňůrce tak, aby vzdálenost od závěsného bodu šňůry ke středu míče byla L= 1 m. Horizontálně letící s rychlostí zasáhne míč PROTI 1 =400 slečna hmotnost střely m= 10 G, který propíchne kuličku přesně v průměru a rychlostí z ní vyletí PROTI 2 =230 slečna. Určete úhel  maximální odchylka zavěšení od svislice. Ignorujte odpor vzduchu a dobu průniku střely.

18. Na rovině skloněné k horizontu pod úhlem α jsou dvě hmotná tělesa m. Součinitel tření mezi tělesy a rovinou k>tg A. Těla mají stejnou rychlost přibližování PROTI. V jaké maximální počáteční vzdálenosti L mezi těly, která se srazí?

19. Vozík sjíždí po hladkých kolejnicích a vytváří svislou smyčku o poloměru R. Jaká je minimální výška H min musí vozík sjet dolů, aby neopustil kolejnice po celé délce? Jaký bude pohyb vozíku, pokud se skutálí z výšky dolů h, menší H min?

20. Určete sílu působící na svislou stěnu ze strany padající činky v okamžiku, kdy osa činky svírá s horizontem úhel . Činka začíná svůj pohyb z vertikální polohy bez počáteční rychlosti. Hmotnost každé činkové koule m.

21. Na niti délky 2 h zavěšené závaží m. Na dálku h pod závěsný bod je zaražen hřebík. Závit byl vychýlen z rovnovážné polohy o úhel /2 a uvolněn. Jaká je maximální výška, do které se závaží zvedne po průchodu rovnovážnou polohou?

22. Hromadný stojan M s polokulovým poloměrem zářezu R stojí na hladké vodorovné rovině. Malé hmotné tělo m nasaďte na okraj zářezu a pusťte. Najděte rychlosti tělesa a stojanu, sílu působící na těleso v okamžiku projetí spodního bodu

23. Zatížení hmoty m, zavěšené na ztužující pružině k, je držen stojanem tak, že pružina je v nedeformovaném stavu. Stojan je náhle odstraněn. Najděte maximální prodloužení pružiny a maximální rychlost zatížení.

24. Od břemene zavěšeného na ztužující pružině k, část hmoty se odtrhne m. Do jaké výšky se pak zvedne zbytek nákladu?

25. Jakou silou byste měli přitlačit na horní váhu hmoty m na nižší váhu M spojené s horní výztužnou pružinou k, zvedl z podlahy po ukončení síly?

26. Dvě tělesa o hmotnosti leží na vodorovné rovině m 1 a m 2 spojené nedeformovanou pružinou. Najděte nejmenší konstantní sílu, která musí být aplikována na levé těleso, aby se pohnulo pravým tělesem. Součinitel tření těles v rovině .

práce výsledných sil působících na těleso se rovná změně kinetické energie tělesa.

Protože změna kinetické energie je rovna práci síly (3), vyjadřuje se kinetická energie tělesa ve stejných jednotkách jako práce, tedy v joulech.

Je-li počáteční rychlost tělesné hmoty m je nula a těleso zvýší svou rychlost na hodnotu υ , pak se práce síly rovná konečné hodnotě kinetické energie tělesa:

A=Ek 2−Ek 1=m⋅υ 22−0=m⋅υ 22 .

42) Potenciální pole

Potenciální pole

konzervativní pole, vektorové pole, jehož cirkulace podél jakékoli uzavřené trajektorie je nulová. Je-li P. p. silové pole, pak to znamená, že práce sil pole po uzavřené trajektorii je rovna nule. Pro P. p. A(M) existuje taková jednohodnotová funkce u(M)(Potenciál pole), který A= stupeň u(viz Gradient). Pokud je PP dán v jednoduše spojené doméně Ω, pak potenciál tohoto pole lze najít vzorcem

kde DOPOLEDNE- jakákoli hladká křivka spojující pevný bod ALE od Ω s tečkou M, t - jednotkový vektor tečné křivky DOPOLEDNE a / - délka oblouku dopoledne, počítáno od bodu ALE. Pokud A(M) - P. p., pak hniloba A= 0 (viz vír vektorového pole). Naopak pokud hniloba A= 0 a pole je definováno v jednoduše spojené doméně a je tedy diferencovatelné A(M) - P. p. Potenciál jsou např. elektrostatické pole, gravitační pole, pole rychlostí při irotačním pohybu.

43) Potenciální energie

Potenciální energie- skalární fyzikální veličina, která charakterizuje schopnost určitého tělesa (nebo hmotného bodu) konat práci díky tomu, že je v poli působení sil. Další definice: potenciální energie je funkcí souřadnic, což je termín v Lagrangeově systému a popisuje interakci prvků systému. Termín „potenciální energie“ zavedl v 19. století skotský inženýr a fyzik William Rankine.

Jednotkou SI pro energii je Joule.

Potenciální energie se bere rovna nule pro nějakou konfiguraci těles v prostoru, jejíž výběr je určen pohodlností dalších výpočtů. Proces výběru této konfigurace se nazývá normalizace potenciální energie.

Správnou definici potenciální energie lze uvést pouze v poli sil, jejichž práce závisí pouze na počáteční a konečné poloze tělesa, nikoli však na trajektorii jeho pohybu. Takové síly se nazývají konzervativní.

Potenciální energie je také charakteristická pro interakci několika těles nebo tělesa a pole.

Jakýkoli fyzikální systém směřuje ke stavu s nejnižší potenciální energií.

Potenciální energie pružné deformace charakterizuje interakci mezi částmi těla.

Potenciální energie v gravitačním poli Země v blízkosti povrchu je přibližně vyjádřena vzorcem:

kde Ep- potenciální energie těla, m- tělesná hmotnost, G- gravitační zrychlení, h- výška polohy těžiště tělesa nad libovolně zvolenou nulovou úrovní.

44) Vztah mezi silou a potenciální energií

Každý bod potenciálního pole odpovídá na jedné straně určité hodnotě vektoru síly působící na těleso a na druhé straně určité hodnotě potenciální energie. Proto musí existovat určitý vztah mezi silou a potenciální energií.

Abychom toto spojení nastolili, vypočítáme elementární práci sil pole při malém posunutí tělesa v libovolně zvoleném směru v prostoru, který označíme písmenem . Tato práce je

kde je průmět síly na směr .

Protože v tomto případě je práce vykonána kvůli zásobě potenciální energie, rovná se ztrátě potenciální energie na segmentu osy:

Z posledních dvou výrazů dostáváme

Poslední výraz udává průměrnou hodnotu intervalu. Na

abyste získali hodnotu v bodě, musíte přejít na limit:

v matematice vektoru,

kde a je skalární funkce x, y, z, se nazývá gradient této skaláry a značí se symbolem . Síla je tedy rovna gradientu potenciální energie s opačným znaménkem

45) Zákon zachování mechanické energie