Teorema despre energia cinetică și potențială. Biblioteca deschisă - bibliotecă deschisă de informații educaționale

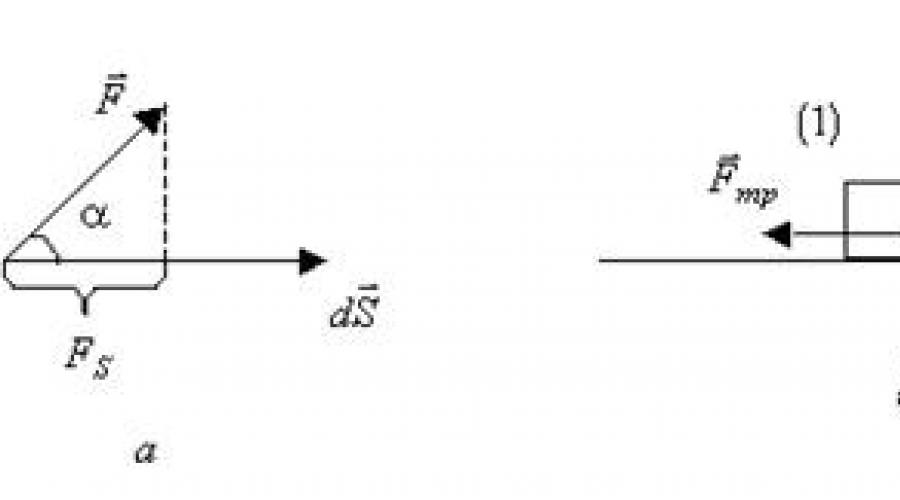
Lucrul elementar dA efectuat de o forță asupra unei deplasări elementare este o mărime egală cu produsul scalar al

unde unghiul a este unghiul dintre vectorii forță și deplasare (Fig. 1.22, a);

Modul vectorial de deplasare elementară sau cale elementară trecut de punctul de aplicare a forței.

Munca efectuată de o forță asupra unei deplasări finale este egală cu suma lucrărilor elementare:

. (1.61)

Dacă forța este constantă ( =const), atunci lucrul ei pe o secțiune dreaptă de lungime l se va scrie după cum urmează:

. (1.62)

Lucrul efectuat de o forță poate fi pozitiv, negativ sau nul. Astfel, lucrul forțelor constante aplicate corpului (Fig. 1.22b) pe secțiunea orizontală a traseului l este egal cu:

Pentru a introduce conceptul de energie kinetică W k corp, să notăm lucrarea elementară dA forțe sub altă formă (vezi 1.2.2):

Atunci pentru munca forței care transferă corpul din starea 1 (viteza corpului) în starea 2 (viteza corpului) putem scrie:

Din formula rezultată rezultă că munca forței este egală cu diferența dintre două mărimi care determină starea inițială (viteză) și finală (viteză) a corpului. În acest caz, condițiile de trecere de la starea 1 la starea 2 nu afectează expresia scrisă. Prin urmare, putem introduce funcția de stare a corpului, energia sa cinetică W as SPV, care caracterizează capacitatea unui corp de a lucra prin schimbarea vitezei de mișcare a acestuia și egală cu

În această expresie, se alege o valoare constantă, presupunând că la viteza zero de mișcare a unui corp energia sa cinetică este zero, prin urmare

Energia cinetică a corpurilor nu depinde de modul în care a fost atinsă o anumită viteză u este o funcție de starea corpului, mărime pozitivă care depinde de alegerea sistemului de referință.

Introducerea lui W k ne permite să formulăm o teoremă despre energia cinetică, conform căreia suma algebrică a muncii tuturor forțelor care acționează asupra unui corp este egală cu creșterea energiei cinetice a corpului:

Această teoremă este utilizată pe scară largă pentru a analiza interacțiunea corpurilor nu numai în mecanică, ci și în alte secțiuni ale cursurilor de fizică, cum ar fi electrostatică, curent continuu, electromagnetism, oscilații și unde etc.

1.4.2. Energia cinetică a unui a.t.t.

Să luăm un a.t.t care se rotește în jurul unei axe fixe cu viteză unghiulară (Fig. 1.16, b). Să ne imaginăm corpul ca pe o colecție de m.t. mase dm, atunci pentru energia cinetică a corpului putem scrie:

Deci, energia cinetică a.t.t. rotirea față de o axă fixă ​​de rotație, este determinată de formula

Dacă un corp participă simultan la mișcări de translație (plat) și de rotație (de exemplu, mișcarea unui cilindru fără alunecare de-a lungul unui plan, Fig. 1.23, a), atunci energia sa cinetică poate fi obținută

Fig.1.23

ca suma energiei cinetice a mișcării de translație a unui corp împreună cu axa de rotație care trece prin centrul său de masă (punctul DESPRE), cu viteza și mișcarea de rotație a corpului față de această axă cu viteza unghiulară

. (1.67)

Pentru solid ( eu 1=1/2mR 2) și cu pereți subțiri ( eu 2=mR 2) cilindri de aceeași masă m si raza R energiile cinetice se vor scrie astfel:

.

Formulele rezultate pentru energia cinetică a cilindrilor fac posibilă explicarea experimentului prin diferența de timp de rulare a acestora în jos dintr-un plan înclinat cu înălțime. h si lungime l(Fig. 1.23, b). Astfel, conform legii conservării energiei (forța de frecare în timpul mișcării cilindrilor poate fi practic neglijată), obținem

,

unde se notează vitezele cilindrilor plini și goali la baza planului înclinat.

Când cilindrii rulează, centrul lor de masă se mișcă uniform accelerat fără o viteză inițială și, prin urmare, conform formulei (1.13), putem scrie:

,

acestea. Este nevoie de mai mult pentru a rula un cilindru gol decât un cilindru solid.

Calitativ, acest lucru poate fi explicat prin faptul că un cilindru gol este mai inert decât unul solid (pentru acesta momentul de inerție față de axa de rotație este mai mare) și, prin urmare, își schimbă viteza mai lent și, prin urmare, petrece mai mult timp. rostogolindu-se în jos pe planul înclinat.

După cum se poate observa din Fig. 1.23, a, modulele de viteză ale punctelor de pe suprafața cilindrului vor fi diferite (u B =0, , u A =2u) datorită faptului că aceste puncte participă simultan atât la mișcări de translație cât și de rotație la viteze Și , și pentru fiecare punct este îndreptat tangent la suprafața cilindrului și este egal ca mărime u( ).

Rețineți că mișcarea cilindrului poate fi considerată și ca o serie de rotații succesive în jurul axei instantanee care trece prin punctul CU(Fig. 1.23, a) cu viteza unghiulară w. Mai mult, în acest caz, energia cinetică a corpului este determinată și de formula (1.67).

Energie este o mărime fizică scalară care este o singură măsură diferite forme mișcarea materiei și măsura trecerii mișcării materiei de la o formă la alta.

Pentru a caracteriza diverse forme de mișcare a materiei se introduc tipurile de energie corespunzătoare, de exemplu: mecanică, internă, energie electrostatică, interacțiuni intranucleare etc.

Energia se supune legii conservării, care este una dintre cele mai importante legi ale naturii.

Energia mecanică E caracterizează mișcarea și interacțiunea corpurilor și este o funcție a vitezelor și a pozițiilor relative ale corpurilor. Este egală cu suma energiilor cinetice și potențiale.

Energie kinetică

Să luăm în considerare cazul în care un corp de masă m există o forță constantă \(~\vec F\) (poate fi rezultanta mai multor forțe), iar vectorii forței \(~\vec F\) și deplasarea \(~\vec s\) sunt direcționați de-a lungul unei linie dreaptă într-o direcție. În acest caz, munca efectuată de forță poate fi definită ca A = F∙s. Modulul de forță conform celei de-a doua legi a lui Newton este egal cu F = m∙a, și modulul de deplasare sîn mişcare rectilinie uniform accelerată este asociat cu modulele iniţialei υ 1 si finala υ 2 viteze si acceleratii A expresia \(~s = \frac(\upsilon^2_2 - \upsilon^2_1)(2a)\) .

De aici ne apucăm de treabă

\(~A = F \cdot s = m \cdot a \cdot \frac(\upsilon^2_2 - \upsilon^2_1)(2a) = \frac(m \cdot \upsilon^2_2)(2) - \frac (m \cdot \upsilon^2_1)(2)\) . (1)

Se numește o mărime fizică egală cu jumătate din produsul masei unui corp și pătratul vitezei acestuia energia cinetică a corpului.

Energia cinetică este reprezentată de literă E k.

\(~E_k = \frac(m \cdot \upsilon^2)(2)\) . (2)

Atunci egalitatea (1) poate fi scrisă după cum urmează:

\(~A = E_(k2) - E_(k1)\) . (3)

Teorema energiei cinetice

munca forțelor rezultante aplicate corpului este egală cu modificarea energiei cinetice a corpului.

Deoarece modificarea energiei cinetice este egală cu munca forței (3), energia cinetică a unui corp este exprimată în aceleași unități ca și munca, adică în jouli.

Dacă viteza iniţială de mişcare a unui corp de masă m este zero și corpul își crește viteza până la valoarea υ , atunci munca efectuată de forță este egală cu valoarea finală a energiei cinetice a corpului:

\(~A = E_(k2) - E_(k1)= \frac(m \cdot \upsilon^2)(2) - 0 = \frac(m \cdot \upsilon^2)(2)\) . (4)

Sensul fizic al energiei cinetice

Energia cinetică a unui corp care se mișcă cu viteza v arată cât de multă muncă trebuie făcută de o forță care acționează asupra unui corp în repaus pentru a-i conferi această viteză.

Energie potențială

Energie potențială este energia interacțiunii dintre corpuri.

Energia potențială a unui corp ridicat deasupra Pământului este energia de interacțiune dintre corp și Pământ prin forțele gravitaționale. Energia potențială a unui corp deformat elastic este energia de interacțiune a părților individuale ale corpului între ele prin forțe elastice.

Potenţial sunt numite putere, al cărui lucru depinde numai de poziția inițială și finală a unui punct sau corp material în mișcare și nu depinde de forma traiectoriei.

Într-o traiectorie închisă, munca efectuată de forța potențială este întotdeauna zero. Forțele potențiale includ forțele gravitaționale, forțele elastice, forțele electrostatice și unele altele.

Puterile, al căror lucru depinde de forma traiectoriei, se numesc nepotenţial. Când un punct sau un corp material se mișcă de-a lungul unei traiectorii închise, munca efectuată de forța nepotențială nu este egală cu zero.

Energia potențială de interacțiune a unui corp cu Pământul

Să găsim munca făcută de gravitație F t la deplasarea unui corp de masă m vertical în jos de la înălțime h 1 deasupra suprafeței Pământului până la o înălțime h 2 (Fig. 1). Dacă diferența h 1 – h 2 este neglijabilă în comparație cu distanța până la centrul Pământului, apoi cu forța gravitațională F t în timpul mișcării corpului poate fi considerat constant și egal mg.

Deoarece deplasarea coincide în direcție cu vectorul gravitațional, munca efectuată de gravitație este egală cu

\(~A = F \cdot s = m \cdot g \cdot (h_1 - h_2)\) . (5)

Să luăm acum în considerare mișcarea unui corp de-a lungul unui plan înclinat. La deplasarea unui corp pe un plan înclinat (Fig. 2), forța gravitației F t = m∙g merge

\(~A = m \cdot g \cdot s \cdot \cos \alpha = m \cdot g \cdot h\) , (6)

Unde h– înălțimea planului înclinat, s– modul de deplasare egal cu lungimea planului înclinat.

Mișcarea unui corp dintr-un punct ÎN exact CU de-a lungul oricărei traiectorii (Fig. 3) poate fi imaginat mental ca fiind constând din mișcări de-a lungul secțiunilor de planuri înclinate cu diferite înălțimi h’, h'' etc. Munca A gravitația tot drumul de la ÎN V CU egală cu suma lucrărilor pe secțiuni individuale ale traseului:

\(~A = m \cdot g \cdot h" + m \cdot g \cdot h"" + \ldots + m \cdot g \cdot h^n = m \cdot g \cdot (h" + h"" + \ldots + h^n) = m \cdot g \cdot (h_1 - h_2)\), (7)

Unde h 1 și h 2 – înălțimile față de suprafața Pământului la care sunt situate, respectiv, punctele ÎNȘi CU.

Egalitatea (7) arată că munca gravitației nu depinde de traiectoria corpului și este întotdeauna egală cu produsul dintre modulul gravitațional și diferența de înălțimi în pozițiile inițiale și finale.

Când vă deplasați în jos, munca gravitației este pozitivă, când vă deplasați în sus este negativă. Lucrul efectuat de gravitație pe o traiectorie închisă este zero.

Egalitatea (7) poate fi reprezentată după cum urmează:

\(~A = - (m \cdot g \cdot h_2 - m \cdot g \cdot h_1)\) . (8)

O mărime fizică egală cu produsul dintre masa unui corp prin modulul de accelerație al căderii libere și înălțimea la care corpul este ridicat deasupra suprafeței Pământului se numește energie potențială interacțiunea dintre corp și Pământ.

Lucru efectuat de gravitație la mișcarea unui corp de masă m dintr-un punct situat la înălţime h 2, până la un punct situat la înălțime h 1 de la suprafața Pământului, de-a lungul oricărei traiectorii, este egală cu modificarea energiei potențiale de interacțiune dintre corp și Pământ, luată cu semnul opus.

\(~A = - (E_(p2) - E_(p1))\) . (9)

Energia potențială este indicată prin literă E p.

Valoarea energiei potențiale a unui corp ridicat deasupra Pământului depinde de alegerea nivelului zero, adică de înălțimea la care se presupune că energia potențială este zero. De obicei, se presupune că energia potențială a unui corp de pe suprafața Pământului este zero.

Cu această alegere a nivelului zero, energia potențială E p unui corp situat la o înălțime h deasupra suprafeței Pământului, egal cu produsul masei m a corpului prin accelerația absolută a căderii libere g si distanta h de la suprafața Pământului:

\(~E_p = m \cdot g \cdot h\) . (10)

Semnificația fizică a energiei potențiale de interacțiune a unui corp cu Pământul

energia potențială a unui corp asupra căruia acționează gravitația este egală cu munca efectuată de gravitație la deplasarea corpului la nivelul zero.

Spre deosebire de energia cinetică a mișcării de translație, care poate avea doar valori pozitive, energia potențială a unui corp poate fi atât pozitivă, cât și negativă. Masa corpului m, situat la o înălțime h, Unde h < h 0 (h 0 – înălțime zero), are energie potențială negativă:

\(~E_p = -m \cdot g \cdot h\) .

Energia potențială a interacțiunii gravitaționale

Energia potențială a interacțiunii gravitaționale a unui sistem de două puncte materiale cu mase mȘi M, situat la distanta r unul din celălalt este egal

\(~E_p = G \cdot \frac(M \cdot m)(r)\) . (unsprezece)

Unde G este constanta gravitațională și zero al referinței de energie potențială ( E p = 0) acceptat la r = ∞.

Energia potențială a interacțiunii gravitaționale a unui corp cu masa m cu Pământul, unde h- înălțimea corpului deasupra suprafeței Pământului, M e – masa Pământului, R e este raza Pământului, iar zero al citirii energiei potențiale este ales la h = 0.

\(~E_e = G \cdot \frac(M_e \cdot m \cdot h)(R_e \cdot (R_e +h))\) . (12)

În aceeași condiție de alegere a referinței zero, energia potențială a interacțiunii gravitaționale a unui corp cu masa m cu Pământul pentru altitudini joase h (h « R e) egal

\(~E_p = m \cdot g \cdot h\),

unde \(~g = G \cdot \frac(M_e)(R^2_e)\) este modulul de accelerație gravitațională lângă suprafața Pământului.

Energia potențială a unui corp deformat elastic

Să calculăm munca efectuată de forța elastică atunci când deformația (alungirea) arcului se modifică de la o valoare inițială X 1 până la valoarea finală X 2 (Fig. 4, b, c).

Forța elastică se modifică pe măsură ce arcul se deformează. Pentru a afla munca efectuată de forța elastică, puteți lua valoarea medie a modulului forței (deoarece forța elastică depinde liniar de X) și înmulțiți cu modulul deplasării:

\(~A = F_(upr-cp) \cdot (x_1 - x_2)\) , (13)

unde \(~F_(upr-cp) = k \cdot \frac(x_1 - x_2)(2)\) . De aici

\(~A = k \cdot \frac(x_1 - x_2)(2) \cdot (x_1 - x_2) = k \cdot \frac(x^2_1 - x^2_2)(2)\) sau \(~A = -\left(\frac(k \cdot x^2_2)(2) - \frac(k \cdot x^2_1)(2) \right)\) . (14)

Se numește o mărime fizică egală cu jumătate din produsul rigidității unui corp prin pătratul deformării acestuia energie potențială corp deformat elastic:

\(~E_p = \frac(k \cdot x^2)(2)\) . (15)

Din formulele (14) și (15) rezultă că munca forței elastice este egală cu modificarea energiei potențiale a unui corp deformat elastic, luată cu semnul opus:

\(~A = -(E_(p2) - E_(p1))\) . (16)

Dacă X 2 = 0 și X 1 = X, atunci, după cum se poate vedea din formulele (14) și (15),

\(~E_p = A\) .

Semnificația fizică a energiei potențiale a unui corp deformat

energia potențială a unui corp deformat elastic este egală cu munca efectuată de forța elastică atunci când corpul trece într-o stare în care deformația este zero.

Energia potențială caracterizează corpurile care interacționează, iar energia cinetică caracterizează corpurile în mișcare. Atât energia potențială, cât și cea cinetică se schimbă numai ca urmare a unei astfel de interacțiuni a corpurilor în care forțele care acționează asupra corpurilor lucrează altfel decât zero. Să luăm în considerare problema schimbărilor de energie în timpul interacțiunilor corpurilor care formează un sistem închis.

Sistem inchis- acesta este un sistem asupra căruia nu se acționează forțele externe sau acțiunea acestor forțe este compensată. Dacă mai multe corpuri interacționează între ele numai prin forțe gravitaționale și forțe elastice și nicio forță externă nu acționează asupra lor, atunci pentru orice interacțiune a corpurilor, munca forțelor elastice sau forțelor gravitaționale este egală cu modificarea energiei potențiale a corpurilor. , luat cu semnul opus:

\(~A = -(E_(p2) - E_(p1))\) . (17)

Conform teoremei energiei cinetice, munca efectuată de aceleași forțe este egală cu modificarea energiei cinetice:

\(~A = E_(k2) - E_(k1)\) . (18)

Dintr-o comparație a egalităților (17) și (18) este clar că modificarea energiei cinetice a corpurilor într-un sistem închis este egală în valoare absolută cu modificarea energiei potențiale a sistemului de corpuri și opus în semn:

\(~E_(k2) - E_(k1) = -(E_(p2) - E_(p1))\) sau \(~E_(k1) + E_(p1) = E_(k2) + E_(p2) \) . (19)

Legea conservării energiei în procesele mecanice:

suma energiei cinetice și potențiale a corpurilor care alcătuiesc un sistem închis și interacționează între ele prin forțe gravitaționale și elastice rămâne constantă.

Se numește suma energiei cinetice și potențiale a corpurilor energie mecanică totală.

Să facem un experiment simplu. Să aruncăm o minge de oțel în sus. Dând viteza inițială υ inch, îi vom da energie cinetică, motiv pentru care va începe să crească în sus. Acțiunea gravitației duce la o scădere a vitezei mingii și, prin urmare, a energiei sale cinetice. Dar mingea se ridică din ce în ce mai sus și capătă din ce în ce mai multă energie potențială ( E p = m∙g∙h). Astfel, energia cinetică nu dispare fără urmă, ci este transformată în energie potențială.

În momentul atingerii punctului de vârf al traiectoriei ( υ = 0) mingea este complet lipsită de energie cinetică ( E k = 0), dar în același timp energia sa potențială devine maximă. Apoi mingea își schimbă direcția și se mișcă în jos cu viteza crescândă. Acum energia potențială este convertită înapoi în energie cinetică.

Legea conservării energiei relevă sens fizic concepte muncă:

munca forțelor gravitaționale și elastice, pe de o parte, este egală cu o creștere a energiei cinetice și, pe de altă parte, cu o scădere a energiei potențiale a corpurilor. Prin urmare, munca este egală cu energia convertită de la un tip la altul.

Legea schimbării energiei mecanice

Dacă un sistem de corpuri care interacționează nu este închis, atunci energia sa mecanică nu este conservată. Modificarea energiei mecanice a unui astfel de sistem este egală cu munca forțelor externe:

\(~A_(vn) = \Delta E = E - E_0\) . (20)

Unde EȘi E 0 – energiile mecanice totale ale sistemului în starea finală, respectiv inițială.

Un exemplu de astfel de sistem este un sistem în care, împreună cu forțele potențiale, acționează forțe nepotențiale. Forțele nepotențiale includ forțele de frecare. În cele mai multe cazuri, atunci când unghiul dintre forța de frecare F r corpul este π radiani, munca efectuată de forța de frecare este negativă și egală cu

\(~A_(tr) = -F_(tr) \cdot s_(12)\) ,

Unde s 12 – calea corpului între punctele 1 și 2.

Forțele de frecare în timpul mișcării unui sistem reduc energia cinetică a acestuia. Ca urmare a acestui fapt, energia mecanică a unui sistem închis neconservativ scade întotdeauna, transformându-se în energia formelor de mișcare nemecanice.

De exemplu, o mașină care se deplasează de-a lungul unei secțiuni orizontale a drumului, după ce a oprit motorul, parcurge o anumită distanță și se oprește sub influența forțelor de frecare. Energia cinetică a mișcării înainte a mașinii a devenit zero, dar energia potențială nu a crescut. Când mașina frâna, plăcuțele de frână, anvelopele și asfaltul s-au încălzit. În consecință, ca urmare a acțiunii forțelor de frecare, energia cinetică a mașinii nu a dispărut, ci s-a transformat în energia internă a mișcării termice a moleculelor.

Legea conservării și transformării energiei

În orice interacțiune fizică, energia este transformată dintr-o formă în alta.

Uneori unghiul dintre forța de frecare F tr și deplasarea elementară Δ r este egal cu zero și munca efectuată de forța de frecare este pozitivă:

\(~A_(tr) = F_(tr) \cdot s_(12)\) ,

Exemplul 1. Lasă forța externă F actioneaza asupra blocului ÎN, care poate aluneca pe cărucior D(Fig. 5). Dacă căruciorul se mișcă spre dreapta, atunci munca efectuată de forța de frecare de alunecare F tr2 care acționează asupra căruciorului din lateralul blocului este pozitiv:

Exemplul 2. Când o roată se rostogolește, forța sa de frecare de rulare este direcționată de-a lungul mișcării, deoarece punctul de contact al roții cu suprafața orizontală se mișcă în direcția opusă direcției de mișcare a roții, iar munca forței de frecare este pozitivă. (Fig. 6):

Literatură

1. Kabardin O.F. Fizica: Referință. materiale: manual. manual pentru elevi. – M.: Educație, 1991. – 367 p.
2. Kikoin I.K., Kikoin A.K. Fizica: manual. pentru clasa a IX-a. medie şcoală – M.: Prosveshchenie, 1992. – 191 p.
3. Manual de fizică elementară: Proc. indemnizatie. În 3 volume / Ed. G.S. Landsberg: vol. 1. Mecanica. Căldură. Fizica moleculară. – M.: Fizmatlit, 2004. – 608 p.
4. Yavorsky B.M., Seleznev Yu.A. Un ghid de referință pentru fizică pentru cei care intră în universități și autoeducație. – M.: Nauka, 1983. – 383 p.

Setați valorile greutății corporale folosind glisoarelem, unghiul de înclinare planA, forta externa F ext , coeficient de frecaremși accelerație A indicate în tabelul 1 pentru echipa dumneavoastră.

În același timp, porniți cronometrul și apăsați butonul „Start”. Opriți cronometrul când corpul dumneavoastră se oprește la capătul planului înclinat.

Faceți acest experiment de 10 ori și înregistrați rezultatele măsurării timpului în care corpul alunecă din planul înclinat în tabel. 2.

TABEL 1. Parametrii inițiali ai experimentului

TABEL 2. Rezultatele măsurătorilor și calculelor

D) - lucrul forţei de frecare pe secţiunea de coborâre;

E) - munca de forta externa pe sectiunea de coborare

și scrieți aceste valori în rândurile corespunzătoare ale tabelului. 2. Calculați valorile medii ale acestor parametri și notați-le în coloana „valori medii” din tabelul 2.

Folosind formula (7), verificați îndeplinirea legii conservării energiei mecanice atunci când un corp se mișcă de-a lungul unui plan înclinat. Calculați erorile și trageți concluzii pe baza rezultatelor experimentelor.

Întrebări și sarcini pentru autocontrol

1.Care este legea conservării energiei mecanice?

2.Pentru ce sisteme se aplică legea conservării energiei mecanice?

3.Care este diferența dintre conceptele de energie și muncă?

4.Ce cauzează schimbarea energiei potențiale?

5.Ce cauzează modificarea energiei cinetice?

6. Este necesar să se îndeplinească condiția de închidere a unui sistem mecanic de corpuri pentru a se îndeplini legea conservării energiei mecanice?

7.Ce forțe se numesc conservatoare?

8.Ce forțe se numesc disipative?

9. Corpul este târât încet pe munte. Forma profilului de munte depinde de: a) munca gravitatiei; b) lucru efectuat de forța de frecare? Punctele de început și de sfârșit ale mișcării corpului sunt fixe.

10. Un corp alunecă din vârful unui plan înclinat fără o viteză inițială. Lucrează forța de frecare de-a lungul întregului traseu de mișcare a corpului până când se oprește pe secțiunea orizontală: a) pe unghiul de înclinare al planului; b) asupra coeficientului de frecare?

11. Două corpuri alunecă pe un plan înclinat de la aceeași înălțime: unul cu o masă m , altul cu masa 2 m . Care corp va parcurge cea mai lungă distanță de-a lungul secțiunii orizontale pentru a se opri și de câte ori? Coeficienții de frecare pentru ambele corpuri sunt aceiași.

12.Sanie de masa m s-a rostogolit pe un munte de înălțimea H și s-a oprit pe o secțiune orizontală. Ce lucrări trebuie făcute pentru a le ridica pe munte de-a lungul liniei pantei.

13. Cu aceeaşi viteză iniţială, corpul trece: a) o depresiune; b) un tobogan având arce de traiectorie identice și coeficienți de frecare identici. Comparați viteza corpului la sfârșitul traseului în ambele cazuri.

Literatură

1. Trofimova T.I. curs de fizica. Capitolul 3, §§12,13.

Să începem cu o definiție. Loc de munca A putere F la deplasare X al corpului căruia i se aplică este definit ca produsul scalar al vectorilor F Și X .

A= F x= Fxcosα. (2.9.1)

Unde α – unghiul dintre direcțiile de forță și deplasare.

Acum vom avea nevoie de expresia (1.6 a), care a fost obținută pentru o mișcare uniform accelerată. Dar vom trage o concluzie universală, care se numește teorema energiei cinetice. Deci, să rescriem egalitatea (1.6 a)

A· X=(V 2 –V 0 2)/2.

Să înmulțim ambele părți ale ecuației cu masa particulei, obținem

Fx=m(V 2 –V 0 2)/2.

In cele din urma

A= m V 2 /2 – m V 0 2 /2. (2.9.1)

mărimea E= m V 2 /2 se numește energia cinetică a particulei.

Ești obișnuit cu faptul că în geometrie teoremele au propria lor formulare orală. Pentru a ține pasul cu această tradiție, să prezentăm teorema energiei cinetice sub formă de text.

Modificarea energiei cinetice a unui corp este egală cu munca efectuată de toate forțele care acționează asupra acestuia.

Această teoremă este universală, adică este valabilă pentru orice tip de mișcare. Cu toate acestea, dovada sa exactă implică utilizarea calculului integral. Prin urmare, o omitem.

Să luăm în considerare un exemplu de mișcare a unui corp într-un câmp gravitațional. Munca gravitației nu depinde de tipul de traiectorie care leagă punctele de început și de sfârșit, ci este determinată numai de diferența de înălțime în pozițiile de început și de sfârșit:

A=mg( h 1 –h 2). (2.9.2)

Să luăm ca origine un punct din câmpul gravitațional și să luăm în considerare munca efectuată de forța gravitațională atunci când mutăm o particulă în acest punct dintr-un alt punct arbitrar. R, situat la o înălțime h. Această lucrare este egală cu mghși se numește energie potențială E n particule într-un punct R:

E n = mgh (2.9.3)

Acum transformăm egalitatea (2.9.1), teorema mecanică despre energia cinetică ia forma

A= m V 2 /2 – m V 0 2 /2= E p1 - E p2. (2.9.4)

m V 2 /2+ E n2 = m V 0 2 /2+ E p1.

În această egalitate, în partea stângă este suma energiei cinetice și potențiale în punctul final al traiectoriei, iar în dreapta - în punctul inițial.

Această cantitate se numește energie mecanică totală. O vom nota E.

E=E k + E P.

Am ajuns la legea conservării energiei totale: într-un sistem închis, energia totală este conservată.

Cu toate acestea, ar trebui făcută o notă. În timp ce ne uitam la un exemplu de așa-zis forțe conservatoare. Aceste forțe depind doar de poziția în spațiu. Iar munca efectuată de astfel de forțe atunci când se deplasează un corp dintr-o poziție în alta depinde doar de aceste două poziții și nu depinde de cale. Munca efectuată de o forță conservatoare este reversibilă mecanic, adică își schimbă semnul atunci când corpul revine în poziția inițială. Gravitația este o forță conservatoare. În viitor, ne vom familiariza cu alte tipuri de forțe conservatoare, de exemplu, cu forța interacțiunii electrostatice.

Dar în natură există și forţe neconservatoare. De exemplu, forța de frecare de alunecare. Cu cât este mai lungă calea unei particule, cu atât se lucrează mai mult de forța de frecare de alunecare care acționează asupra acestei particule. În plus, munca efectuată de forța de frecare de alunecare este întotdeauna negativă, adică o astfel de forță nu poate „returna” energia.

Pentru sistemele închise, energia totală este, desigur, conservată. Dar pentru majoritatea problemelor din mecanică este mai important un caz special al legii conservării energiei, și anume legea conservării energiei mecanice totale. Iată formularea lui.

Dacă asupra unui corp acționează numai forțele conservatoare, atunci energia sa mecanică totală, definită ca suma energiilor cinetice și potențiale, este conservată..

În cele ce urmează vom avea nevoie de încă două egalități importante. Ca întotdeauna, vom înlocui concluzia cu o simplă demonstrație a unui caz special al câmpului gravitațional. Dar forma acestor egalități va fi valabilă pentru orice forță conservatoare.

Să reducem egalitatea (2.9.4) la forma

A=F∆X= E p1 - E n2 = –( E p.kon – E n.beg)= – ∆U.

Aici ne-am uitat la lucrare A la deplasarea unui corp pe o distanta ∆ X. Valoarea ∆U, egală cu diferența dintre energia potențială finală și inițială, se numește modificarea energiei potențiale. Și egalitatea rezultată merită o linie separată și un număr special. Să ne grăbim să i-o atribuim:

A=– ∆U (2.9.5)

De aici urmează relația matematică dintre forță și energia potențială:

F= – ∆U/∆ X (2.9.6)

În cazul general, fără legătură cu câmpul gravitațional, egalitatea (2.9.6) este cea mai simplă ecuație diferențială

F= – dU/ dx.

Să luăm în considerare ultimul exemplu fără dovezi. Forța gravitațională este descrisă de legea gravitației universale F(r)= GmM/ r 2 si este conservator. Expresia pentru energia potențială a câmpului gravitațional are forma:

U(r)= – GmM/ r.

Autor: – Să ne uităm la un caz simplu. Un corp de masă m situat pe un plan orizontal este acționat asupra unei perioade de timp de T forță orizontală F. Nu există frecare. Care este munca făcută cu forța? F?

Student: – Pe parcursul T corpul se va deplasa pe o distanta S= AT 2/2, unde A=F/m. Prin urmare, locul de muncă cerut este A=F S= F 2 T 2/(2m).

Autor: Totul este corect dacă presupunem că corpul era în repaus înainte ca forța să înceapă să acționeze asupra lui. Să complicăm puțin sarcina. Lăsați corpul să se miște rectiliniu și uniform înainte de apariția forței cu o anumită viteză V 0, co-direcționată cu forța externă. Care este munca făcută la timp acum? T?

Student: – Pentru a calcula deplasarea, voi lua formula mai generală S= V 0 T+AT 2/2, o primesc pentru serviciu A=F(V 0 T+AT 2/2). Comparând cu rezultatul anterior, văd că aceeași forță produce muncă diferită în aceleași perioade de timp.

Un corp de masă m alunecă pe un plan înclinat cu un unghi de înclinare α. Coeficientul de frecare de alunecare a unui corp pe un plan k. O forță orizontală acționează asupra corpului tot timpul F. Care este munca efectuată de această forță atunci când deplasați corpul pe o distanță S?

Student: – Să aranjam forțele și să le găsim rezultanta. Corpul este acționat de o forță externă F, precum și de forțele gravitaționale, reacția suportului și frecarea.

Student: – Se pare că lucrarea A = F S cosα și atât. Am fost foarte dezamăgit de obiceiul de a căuta toate forțele de fiecare dată, mai ales că problema indica masa și coeficientul de frecare.

Student: – Munca de forta F Am calculat deja: A 1 = F S cosα. Lucrul efectuat de gravitație este A 2 =mgS păcatα. Lucrul forței de frecare ... este negativ, deoarece vectorii forței și deplasării sunt direcționați invers: A 3 = – kmgS cosα. Munca forței de reacție N este egal cu zero, deoarece forța și deplasarea sunt perpendiculare. Este adevărat că nu înțeleg cu adevărat sensul muncii negative?

Autor: – Aceasta înseamnă că munca unei forțe date reduce energia cinetică a corpului. Apropo. Să discutăm mișcarea corpului prezentat în fig. 2.9.1 din punctul de vedere al legii conservării energiei. Mai întâi, găsiți munca totală efectuată de toate forțele.

Student: - A= A 1 + A 2 + A 3 = FS cosα+ mgS păcatα– kmgS cosα.

Conform teoremei energiei cinetice, diferența dintre energiile cinetice în starea finală și inițială este egală cu munca efectuată asupra corpului:

E La - E n = A.

Student: – Poate că acestea au fost alte ecuații care nu au legătură cu această problemă?

Autor: – Dar toate ecuațiile ar trebui să dea același rezultat. Ideea este că energia potențială este conținută latentă în expresia pentru lucru total. Într-adevăr, amintiți-vă A 2 = mgS păcatα=mgh, unde h este înălțimea de coborâre a corpului. Acum obțineți din teorema energiei cinetice o expresie pentru legea conservării energiei.

Student: – Deoarece mgh=U n – U k, unde U n și U k sunt, respectiv, energiile potențiale inițiale și finale ale corpului, avem:

m V n 2 /2 + U n + A 1 + A 3 = m V la 2/2+ U La.

Student: – Acest lucru, după părerea mea, este ușor. Munca efectuată de forța de frecare este exact egală ca mărime cu cantitatea de căldură Q. De aceea Q= kmgS cosα.

Student: m V n 2 /2 + U n + A 1 – Q= m V la 2/2+ U La.

Autor: – Să generalizăm acum oarecum definiția muncii. Faptul este că relația (2.9.1) este adevărată numai pentru cazul unei forțe constante. Deși există multe cazuri când forța în sine depinde de mișcarea particulei. Dă un exemplu.

Student: – Primul lucru care îmi vine în minte este întinderea de primăvară. Pe măsură ce capătul liber al arcului se mișcă, forța crește. Al doilea exemplu este legat de un pendul, care, după cum știm, este mai greu de ținut cu abateri mari de la poziția de echilibru.

Autor: – Amenda. Să ne uităm la exemplul de primăvară. Forța elastică a unui arc ideal este descrisă de legea lui Hooke, conform căreia atunci când arcul este comprimat (sau întins) cu o cantitate X apare o forță opusă deplasării, dependentă liniar de X. Să scriem legea lui Hooke ca o egalitate:

F= – k X (2.9.2)

Aici k este coeficientul de rigiditate a arcului, X– cantitatea de deformare a arcului. Desenați un grafic al relației F(X).

Student: Desenul meu este prezentat în imagine.

Fig.2.9.2

Jumătatea stângă a graficului corespunde comprimării arcului, iar jumătatea dreaptă corespunde tensiunii.

Autor: – Acum să calculăm munca efectuată de forța F când trecem de la X=0 la X= S. Există o regulă generală pentru aceasta. Dacă știm dependența generală a forței de deplasare, atunci lucrul pe secțiune depinde de x 1 până la x 2 este aria de sub curbăF(X) pe acest segment.

Student: – Aceasta înseamnă că munca efectuată de forța elastică la mutarea unui corp din X=0 la X=S este negativ, iar modulul său este egal cu aria unui triunghi dreptunghic: A= kS2/2.

A= k X 2 /2. (2.9.3)

Acest lucru este transformat în energia potențială a arcului deformat.

Poveste.

Rutherford le-a demonstrat ascultătorilor degradarea radiului. Ecranul strălucea și se întuneca alternativ.

- Acum Vezi – spuse Rutherford, – că nimic nu se vede. Și de ce nimic nu este vizibil, veți vedea acum.

Întrebări și sarcini

1. Enumerați situațiile întâlnite în viața de zi cu zi în care sunt implicate forțe neconservatoare.

2. Ridiți încet cartea de pe masă pe un raft înalt. Enumerați forțele care acționează asupra cărții și stabiliți care sunt conservatoare și care nu.

3. Forța rezultată care acționează asupra particulei este conservatoare și crește energia cinetică a acesteia cu 300 J. Care este modificarea în a) energia potențială a particulei, b) energia sa totală?

4. Are sens fizic următoarea afirmație: utilizarea stâlpilor din plastic flexibil în sărituri în înălțime a dus la o creștere a rezultatelor datorită faptului că flexibilitatea sa mai mare oferă energie elastică suplimentară, convertită în energie potențială a câmpului gravitațional?

5. Există un plan înclinat, al cărui capăt este ridicat la o înălțime N. Masa corpului M se rostogolește în jos (fără viteza inițială) din punctul de sus. Viteza acestui corp la baza planului înclinat depinde de unghiul pe care îl face cu orizontul, dacă a) nu există frecare, b) există frecare?

6. De ce tot obosim când urcăm mai întâi pe un munte și apoi îl coborâm? La urma urmei, munca totală efectuată într-un câmp gravitațional este zero.

7. Acest exemplu este și mai dur. Imaginați-vă că țineți o gantere la distanță de braț. Nu-ți face griji, nu este foarte greu. Dar totuși mâna obosește. Dar nu există lucru mecanic, pentru că nu există mișcare. Unde se duce energia mușchilor tăi?

8. Masa de arc m se sprijină în poziţie verticală pe masă. Va putea arcul să sară în sus și să iasă de pe masă după ce îl comprimați, apăsând de sus, și apoi îl eliberați? Explicați răspunsul folosind legea conservării energiei.

9. Ce se întâmplă cu energia potențială pe care apa o avea în vârful cascadei când apa ajunge la baza ei? Ce se întâmplă cu energia cinetică și totală?

10. Turiștii cu experiență preferă să calce peste un buștean căzut, decât să calce pe el și să sară de pe partea opusă. Explicați fenomenul.

11. Două persoane se află pe platforme diferite care se mișcă una față de alta cu viteza V. Ei observă un buștean care este tras de-a lungul unei suprafețe orizontale aspre. Coincid valorile obținute de aceste persoane: a) energia cinetică a jurnalului; b) munca totală efectuată asupra corpului; c) energie mecanică transformată în energie termică datorită prezenței frecării? Răspunsul la întrebarea c) contrazice răspunsurile la întrebările a) și b)?

12. De unde vine energia cinetică a unei mașini atunci când accelerează uniform din starea de repaus? Cum putem lega creșterea energiei cinetice de prezența frecării între anvelope și autostradă?

13. Iarna, Pământul se apropie de Soare la cea mai scurtă distanță. Când este cea mai mare energia potențială a Pământului?

14 Energia mecanică totală poate fi negativă? Dă exemple.

15. În ce moment este forța cea mai mare? Pentru fiecare punct numerotat, indicați în ce direcție acționează forța. Care punct corespunde poziției de echilibru?

Sarcini

16. Un glonț pătrunde într-o placă fixă ​​cu o viteză minimă de 200 Domnișoară. Cu ce ​​viteză trebuie să se deplaseze glonțul pentru a străpunge această scândură suspendată pe un fir lung? Greutatea glonțului 15 G, greutatea plăcii 90 G, glonțul lovește exact centrul tablei perpendicular pe suprafața sa.

17. Minge de lemn de masă M =1 kg atârnă pe un șnur astfel încât distanța de la punctul de suspendare al șnurului la centrul mingii să fie egală cu L= 1 m. Mingea este lovită de un avion care zboară orizontal cu viteză V 1 =400 Domnișoară masa gloanțelor m= 10 G, care străpunge mingea exact de-a lungul diametrului și zboară din ea cu o viteză V 2 =230 Domnișoară. Definiți Unghiul  abaterea maximă a suspensiei de la verticală. Neglijați rezistența aerului și timpul necesar pentru ca un glonț să penetreze mingea.

18. Pe un plan înclinat spre orizont sub un unghi α, două corpuri de masă m. Coeficientul de frecare între corpuri și plan k>tgα. Corpurilor li se dau aceleași viteze de contorizare V. La ce distanta maxima initiala L se vor ciocni între cadavre?

19. Căruciorul se rostogolește pe șine netede formând o buclă verticală de rază R. De la ce înălțime minimă H min ar trebui să se rostogolească căruciorul astfel încât să nu părăsească șinele pe toată lungimea lor? Care va fi mișcarea căruciorului dacă se rostogolește de la înălțime? h, mai mic H min?

20. Să se determine forța care acționează asupra peretelui vertical din ganterele care cade în momentul în care axa ganterei formează un unghi  cu orizontala. Gantera își începe mișcarea dintr-o poziție verticală fără o viteză inițială. Masa fiecărei mingi cu gantere este m.

21. Pe un fir de lungime 2 h greutate suspendată m. La distanta h se bate un cui sub punctul de suspendare. Filetul a fost deviat din poziția de echilibru cu un unghi de /2 și eliberat. Până la ce înălțime maximă va crește greutatea după trecerea prin poziția de echilibru?

22. Stand de masă M cu raza de adâncime emisferică R stă pe un plan orizontal neted. Corp mic de masă m Așezați-l pe marginea crestăturii și eliberați-l. Aflați viteza corpului și a suportului, forța care acționează asupra corpului în momentul depășirii punctului cel mai de jos

23. Masa de greutate m, suspendat pe un arc de rigidizare k, este ținut de suport astfel încât arcul să fie într-o stare nedeformată. Suportul este îndepărtat brusc. Aflați alungirea maximă a arcului și viteza maximă a sarcinii.

24. De la o sarcină suspendată pe un arc de rigidizare k, o parte din masă se desprinde m. La ce înălțime se va ridica partea rămasă a încărcăturii după aceasta?

25. Câtă forță trebuie aplicată masei superioare m, astfel încât sarcina inferioară să cântărească M, conectat la arcul de rigidizare superior k, a ieșit de pe podea după ce forța a încetat?

26. Două corpuri cu mase se află pe un plan orizontal m 1 și m 2 legate printr-un arc neformat. Găsiți care este cea mai mică forță constantă care trebuie aplicată corpului stâng pentru ca cel drept să se miște. Coeficientul de frecare dintre corpuri și un plan este .

munca forțelor rezultante aplicate corpului este egală cu modificarea energiei cinetice a corpului.

Deoarece modificarea energiei cinetice este egală cu munca forței (3), energia cinetică a unui corp este exprimată în aceleași unități ca și munca, adică în jouli.

Dacă viteza iniţială de mişcare a unui corp de masă m este zero și corpul își crește viteza până la valoarea υ , atunci munca efectuată de forță este egală cu valoarea finală a energiei cinetice a corpului:

A=Ek 2−Ek 1=m⋅υ 22−0=m⋅υ 22 .

42) Câmpuri potențiale

Câmp potențial

câmp conservator, un câmp vectorial a cărui circulație de-a lungul oricărei traiectorii închise este egală cu zero. Dacă un câmp de forță este un câmp de forță, atunci aceasta înseamnă că munca forțelor câmpului de-a lungul unei traiectorii închise este egală cu zero. Pentru P. p. A(M) există o funcție atât de unică u(M)(Potențial de câmp) că A= grad u(vezi Gradient). Dacă un câmp de câmp este dat într-un domeniu simplu conectat Ω, atunci potențialul acestui câmp poate fi găsit folosind formula

în care A.M- orice curbă netedă care leagă un punct fix A de la Ω cu un punct M, t - vector unitar al curbei tangente A.M.și / - lungimea arcului A.M. bazat pe puncte A. Dacă A(M) - P. p., apoi putrezesc A= 0 (vezi vortexul câmpului vectorial). În schimb, dacă putrezesc A= 0 și câmpul este definit într-un domeniu simplu conectat și este diferențiabil, atunci A(M) - Potențialul P.p. sunt, de exemplu, un câmp electrostatic, un câmp gravitațional și un câmp de viteză în timpul mișcării irrotaționale.

43) Energie potențială

Energie potențială- o mărime fizică scalară care caracterizează capacitatea unui anumit corp (sau punct material) de a lucra datorită poziționării sale în câmpul de acțiune al forțelor. O altă definiție: energia potențială este o funcție de coordonate, care este un termen în sistemul lagrangian și descrie interacțiunea elementelor sistemului. Termenul „energie potențială” a fost inventat în secolul al XIX-lea de către inginerul și fizicianul scoțian William Rankine.

Unitatea de energie din SI este Joule.

Se presupune că energia potențială este zero pentru o anumită configurație de corpuri în spațiu, a cărei alegere este determinată de comoditatea calculelor ulterioare. Procesul de alegere a acestei configurații este numit normalizarea energiei potenţiale.

O definiție corectă a energiei potențiale poate fi dată doar într-un câmp de forțe, a cărui activitate depinde doar de poziția inițială și finală a corpului, dar nu și de traiectoria mișcării acestuia. Astfel de forțe sunt numite conservatoare.

De asemenea, energia potențială este o caracteristică a interacțiunii mai multor corpuri sau a unui corp și a unui câmp.

Orice sistem fizic tinde spre o stare cu cea mai mică energie potențială.

Energia potențială a deformării elastice caracterizează interacțiunea dintre părți ale corpului.

Energia potențială din câmpul gravitațional al Pământului lângă suprafață este exprimată aproximativ prin formula:

Unde E p- energia potențială a corpului, m- masa corpului, g- accelerarea gravitației, h- înălțimea centrului de masă al corpului deasupra unui nivel zero selectat în mod arbitrar.

44) Relația dintre forță și energia potențială

Fiecare punct al câmpului potențial corespunde, pe de o parte, unei anumite valori a vectorului forță care acționează asupra corpului, iar, pe de altă parte, unei anumite valori a energiei potențiale. Prin urmare, trebuie să existe o anumită relație între forță și energia potențială.

Pentru a stabili această legătură, să calculăm munca elementară efectuată de forțele câmpului în timpul unei mici deplasări a corpului care are loc de-a lungul unei direcții alese în mod arbitrar în spațiu, pe care o notăm cu litera . Această lucrare este egală cu

unde este proiecția forței pe direcție.

Deoarece în acest caz lucrarea se face din cauza rezervei de energie potențială, aceasta este egală cu pierderea de energie potențială pe segmentul de axă:

Din ultimele două expresii obținem

Ultima expresie dă valoarea medie a intervalului. La

pentru a obține valoarea în punctul în care trebuie să mergeți la limită:

în vector de matematică,

unde a este o funcție scalară a lui x, y, z, numită gradientul acestui scalar și notat cu simbolul . Prin urmare, forța este egală cu gradientul de energie potențială luat cu semnul opus

45) Legea conservării energiei mecanice